تحليل الارتباط هو كل طريقة إحصائية يتم فيها تخمين متوسط قيمة متغير عشوائي (غير محدد مسبقاً) أو عدة متغيرات عشوائية اعتمادا على قيم وقياسات متغيرات عشوائية أخرى لوجود علاقة متبادلة أو اتصال بين المتغير التابع ومتغير مستقل أو أكثر.، له عدة أنواع مثل: الانحدار الخطي، والانحدار المنطقي، وانحدار بواسون.

من الأمثلة النموذجية على تحليل الانحدار: اعتماد ضغط الدم Y على عمر الشخص X، أو اعتماد الوزن لحيوانات التجربة Y على معدل التغذية اليومي X. هذا الارتباط والتابعية بين X وY هي ما ندعوه بالانحدار أو الارتباط فنقول ارتباط Y ب X.

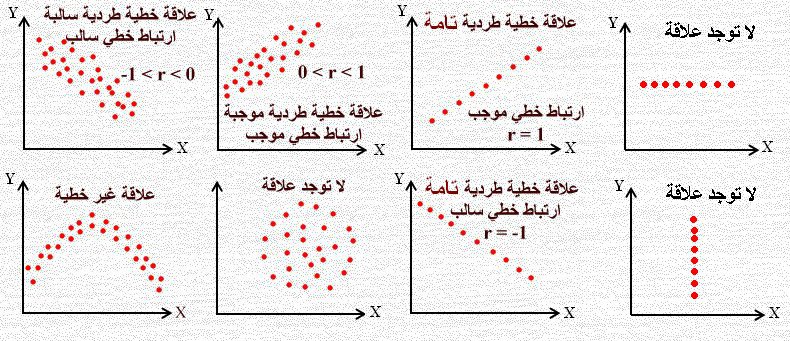
يساعد تحليل الارتباط في تحديد درجة العلاقة بين متغيرين أو أكثر.

يمكن أن يكون الارتباط موجبًا أو سلبيًا.

1. الارتباط الإيجابي:

في هذا ، عندما يتحرك متغيرين في نفس الاتجاه. هذا يعني أنه عندما يزيد أحدهما ، يزداد الآخر أيضًا ، عندما ينقص أحدهما الآخر أيضًا. يسمى هذا النوع من العلاقة الارتباط الإيجابي.

مثال: العلاقة بين الطول والوزن والدخل والنفقات.

1. ارتباط سلبي:

هنا ، عندما يتحرك متغيرين في اتجاهين متعاكسين. هذا يعني أنه عندما يزيد أحدهما ، فإن الآخر سينقص ، وعندما ينقص أحدهما سيزداد الآخر. يسمى هذا النوع من العلاقة الارتباط السلبي.

مثال: العلاقة بين السعر والطلب.

تقيس كل من طريقة كارل بيرسون وطريقة تصنيف سبيرمان الارتباط للبيانات الكمية.

يتراوح معامل الارتباط بطريقتين كارل بيرسون وسبيرمان بين -1 و +1.

تفسير

كانت الاختلافات التالية موجودة ،

1. يقيس أسلوب كارل بيرسون في الارتباط البيانات الكمية ، بينما يقيس أسلوب سبيرمان في ارتباط الرتبة معامل الارتباط للبيانات النوعية.

1. تحسب طريقة كارل بيرسون المشتقات من المتوسط ​​الفعلي ، بينما تحسب طريقة سبيرمان فروق الرتب.

1. يعطي أسلوب كارل بيرسون للارتباط أهمية أكبر للقيمة القصوى بناءً على القيم الفعلية ، بينما تعطي طريقة سبيرمان أهمية أقل للقيمة القصوى لأنها تعطي الترتيب.

الفرق بين الارتباط الخطي وغير الخطي:

الارتباط الخطي:

يقال إن الارتباط الخطي موجود إذا كان مقدار التغيير في متغير واحد يميل إلى تحمل نسبة ثابتة إلى مقدار التغيير في المتغير الآخر. الرسم البياني للمتغيرات التي لها مثل هذه العلاقة سيشكل خطًا مستقيمًا.

الارتباط غير الخطي (المنحني):

في الارتباط غير الخطي أو المنحني يقال إنه موجود إذا كان مقدار التغيير في متغير واحد لا يحمل نسبة ثابتة إلى مقدار التغيير في المتغير الآخر ذي الصلة. الرسم البياني للمتغيرات التي لها مثل هذه العلاقة لن يشكل خطًا مستقيمًا.

يعطي الارتباط الخطي نسبة ثابتة بين متغيرين.

الارتباط غير الخطي لا يعطي نسبة ثابتة بين متغيرين.

1- https://mimirbook.com/ar/5343bcf699c

2-https://www.marefa.org/%D8%AA%D8%AD%D9%84%D9%8A%D9%84_%D8%A7%D9%84%D8%A7%D9%86%D9%83%D9%81%D8%A7%D8%A1

3-https://www.jmasi.com/ehsa/correlation/int.htm