في هذا الدرس ، سنتعرف على مبادئ علم الاحتمالات probabilities , يقولون أن الاحتمال Probability هو عكس الإحصائيات statistics، و بينهما علاقة تكامل .

بعبارة أخرى ، في الإحصائيات ، يتم تزويدنا بالبيانات ونحاول استنتاج الأسباب المحتملة وراء هذة البيانات ، بينما في الاحتمال ، يتم إعطاؤنا وصفًا للأسباب ونرغب في التنبؤ بالبيانات المحتملة.

هدفنا الآن من دراسة الاحتمالات وليس الإحصائيات هو حاجتنا للتعرف أكثر علي المفاهيم والقواعد الازمة لوصف العلاقة بين البيانات والأسباب الكامنة وراءها.

سنستخدم تجربة رمي العملة كمثال توضيحي لاستيعاب مفهوم الاحتمالات probability , وإنشاء بعض البيانات الإحصائية للشرح .

فأي عملة معدنية . لها وجهان ، بصفة عامة يكون أحد الوجهان علية صورة (head) والآخر علية كتابة (tail) , دعنا نقوم برمي العملة في الهواء عدة مرات والتحقق من الوجه الذي يظهر عندما تقع على الأرض . وكانت النتائج التي حصلتُ عليها كالتالي

• الرمية الأولي هي صورة (head)
• الرمية الثانية هي صورة (head)

إذن بيانات الرميات هي {heads, heads}

فلنرميها للمرة الثالثة.

وبصورة لا تصدق ، إنها صورة (head) مرة أخرى.

هل تعتقد أنه إذا رميتُ هذه العملة مرارًا وتكرارًا ، فستظهر دائمًا صورة (head) ؟ مع العلم أن كلا الجانبين لهما فرص متكافئة.

بناءً علي الرميات السابقة يمكنك المجادلة قليلاً ، لكنني أعتقد أنالإجابة الصحيحة هي لا. هذا بسبب ما نسميه بالفرص المتكافئة للوجهين بالإضافة لعدم وجود اي رابط اوعلاقة بين الرميات وهذا يعني أن وجه الكتابة (tail) لديه بالفعل فرصة بنسبة 50٪ في كل رمية , فلنعد رمي العملة للمرة الرابعة

• ونتيجة الرمية الرابعة هي كتابة (tail)

هذه المرة حصلنا علي كتابة (tail) وهذا ليس بمستغرباً لأن كلا الجانبين له فرص متساوية في كل رمية للعملة.

إذاً نتعلم من تلك التجربة البسيطة أن الاحتمال هو طريقة لوصف النتائج المتوقعة لتجربة ما, في مثالنا هنا كان رمي العملة.

دعنا نلقي بعض الضوء علي العملة المتكافئة (fair coin). عند دراسة احتمالية ظهور صورة (head) عند رمي عملة معدنية - بالمُناسبة يتم التعبير عنها بالمعادلة (H) P وتقرأ احتمال ظهور وجهة الصورة (head) للعملة- ،إذا كانت العملة المتكافئة فهذا يعني تساوي الفرص لكيلا الوجهين, وبالتالي سيكون احتمال فرص ظهور وجه الصورة (head) هو 50٪ أو 1/0.5 .

P(HEAD)= 50 %

أي إننا سنفترض نتبجة نصف الرميات يجب أن تكون وجه الصورة (head) - غالبًا تكتب 0.5 ، وهو نصف 1.

بمعني إذا كان الاحتمال ب 1 فهذا يعني أنه يظهر وجه الصورة (head) للعملة دائمًا ، ويعني الاحتمال 0.5 أنه يظهر في نصف عدد الرميات , لذالك دعني أسألكم بماذا تعتقد ان يكون احتمال وجه الكتابة (tail) - (T) P- لهذه العملة؟

طبعا الإجابة من غير تفكير هي 0.5 حيث ان 1 - 0.5= 0.5

لاحظ: في التجربة المتكافئة الغير المتحيزة كل النتائج المحتملة لها نفس نسبة التمثيل بمعني سنقوم بقسمة الواحد علي عددهم .

على الجانب الآخر العملة المتحيزة (غير المتكافئة) (loaded coin) هي عملة تُرجح كافة أحد جوانبها بشكل متكرر أكثر من الآخر.

على سبيل المثال ، افترض أن لدينا عملة معدنية تُرجع دائمًا لوجه لصورة (head).

برأيك ما هو الاحتمال الذي سنقدره لوجه الصورة (head) ؟ ماذا سيكون الرقم الصحيح هنا؟

نعم الإجابة هي الرقم 1 أي ما يعادل 100٪ من الحلات لأنه هو الذي يظهر علي الدوم.

وبالنظر إلى الافتراض السابق ، ما هو الرقم الذي سنقدره الآن لاحتمال وجه الكتابة (tail) ؟

ونعم ، الجواب هو صفر. وهنا نجد قانونًا صغيرًا نرغب في تسليط الضوء عليه ، وهو احتمال ظهور وجه الصورة (head) بالإضافة إلى احتمال وجه الكتابة (tail) يساوي 1 .

P(H) +P(T) = 1

وسبب صحته منطقي فنعلم أن رمي العملة إما يكون الصورة (head) أو الكتابة (tail) ، فلا توجد خيارات أخرى. ، فبتالي فإن فرص حدوث أي منهما هي 1 ، لذلك يمكننا استخدام هذا القانون لحساب احتمال الصورة (head) أو الكتابة (tail) وكذالك لأي لأمثلة أخرى

لنفترض أن احتمال ظهور الصورة (head) هو 0.75 وهو ما يعادل القول لو رمينا العملة 4 مرات فستكون النتيجة 3 مرات لصورة (head) من 4 محاولات . برأيك ما هو احتمال الكتابة (tail)؟

والإجابة هي 0.25 ، وهي 1-0.75 باستخدام القاعدة الموضحة أعلاه كما يمكنك التحقق ،

0.75 + 0.25 = 1.

لا تفقد تركيزك لقد تعلمنا للتو شيئًا مهمًا. فلو هناك احتمال لنتيجة ما؛ ولنسميها A في الوقت الحالي. وتعلمنا من القانون السابق أن احتمالية النتيجة المعاكسة التي سنسميها ¬ -هذا الرمز هنا يعني "ليس A" - هو 1 ناقص احتمال A

تذكر دائماً أن هذا هو قانون الاحتمال الأساسي ، والذي هو مفيدًا جداً لإنجاز كثير من المهام.

P(¬) = 1 - A

فلنلقي العملة مرتين ونراقب نتائج الرميات .بإعتقادك ما هو احتمال رؤية الصورة (head) في كلتا المرتيين بإفتراض أني رميت نفس العملة و كونها غير متحيزة (fair coin) ؟ هذا يعني انه لكل رمية ، نفترض أن احتمال ظهور الصورة (head) هو 0.5.

سيكون الامر محيراً إذا لم تكن قد درست الاحتمالات من قبل ، ولكن الإجابة هي 0.25. ولتسهيل الاجابة سنستخدم مايسمي بمخطط شجرة الاحتمالات . في شجرة الاحتمالات ، تقوم برسم كل نتيجة محتملة للتجربة التي تجريها في شكل هرمي أو فروع شجرية.

هنا في مثالنا لدينا رميتان في الرمية الأولي هناك احتملان وفي الرمية الثانية سيكون لكل احتمال من الرمية الأولي احتملان فيكون كل النتائج المحتملة أربع احتمالات :

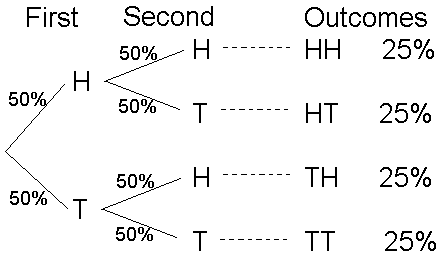
1. الاحتمال الاول سيكون الصورة (head) والصورة (head)
2. الاحتمال الثاني سيكون الصورة (head) و الكتابة (tail)
3. الاحتمال الثالث سيكون الكتابة (tail) والصورة (head)
4. الاحتمال الرابع سيكون الكتابة (tail) و الكتابة (tail)

عندما ننظر إلى هذا المخطط ، يمكنك أن ترى كل النتائج المحتملة لهاتين الرميتين هم أربع نتائج محتملة ، ونحن نفترض أن كلا الوجهين الصورة (head) و الكتابة (tail) متساوية في الاحتمال ، فإن كل واحدة من هذه النتائج محتملة بشكل متساوٍ. نظرًا لأننا نعلم أن مجموع جميع النتائج المحتملة لابد ان يساوي 1 ، فإننا نستنتج أن كل نتيجة لها احتمال 1/4 ، أو 0.25.

طريقة أخرى لتمثيل هذه النتيجة هي ضرب احتمالية ظهور الوجه في كل محاولة .

فما هي احتمالات أن تكون النتيجة الأولى صورة (head) والنتيجة الثانية صورة (head)؟ الأول هو 0.5 ، وكذلك الأخير. إذا ضربنا هذين العددين ، فستكون النتيجة 0.25 أو ربعًا.

P(HH) = 0.5 * 0.5 =0.25

لنعد التجربة ولكن هذة المرة سنستخدم عملة متحيزة (loaded coin) ، وسأفترض أن احتمال ظهور وجة الصورة (head) هو 0.6.

P(H) =0.6

بناءً علي هذا المعطي, ما هو احتمال الحصول علي وجة الكتابة (tail)؟

P(T) =?

والإجابة هي 0.4 لأن احتمال ظهور الصورة هو 0.6

وبما أن كل مجموع كل الاحتمالات لابد ان يساوي1

إذاً P(T)= 1 - 0.6 =0.4

ولآن دعنا نعدل قيم المخطط السابق لحساب احتمالات أن تكون النتيجة الأولى صورة (head) والنتيجة الثانية صورة (head)

P(HH) = ? Where P(H)=0.6

سنعدل قيم شجرة الاحتمالات بالكامل لكل الحلات كالأتي.

باستخدام قاعدة الضرب

1. الاحتمال الاول هو الصورة (head) والصورة (head) --> هي 0.6 * 0.6 ،فتكون النتيجة 0.36.
2. الاحتمال الثاني هو الصورة (head) و الكتابة (tail) --> هي 0.6 * 0.4 ،فتكون النتيجة 0.24.
3. الاحتمال الثالث هو الكتابة (tail) والصورة (head) --> هي 0.4 * 0.6 ،فتكون النتيجة 0.24..
4. الاحتمال الرابع هو الكتابة (tail) و الكتابة (tail) --> هي 0.4 * 0.4 ،فتكون النتيجة 0.16.

إذا جمعت ناتج عمليات الضرب أعلاه - لابد ان يكون ناتج الجمع هو 1

شجرة الاحتمالات تأخذ في الاعتبار جميع الحالات الممكنة فلابد لمجموع الاحتمالات أن يكون 1 دائمًا ، وجميع الحالات الممكنة معًا لها احتمال 1 كما عرفنا سابقا

الآن دعنا نذهب إلى أقصى حدود التحيز ،و نفترض أن احتمال الحصول على الصورة (head) هو 1 ، ما هو احتمال ( الصورة (head) ، الصورة (head)) ؟

P(H,H) =?

والإجابة هي 1.

بالفعل أننا نعلم أن احتمال الحصول على الكتابة (tail) هو 0. فكل الاحتمالات لصالح الصورة (head).

ومن السهل التحقق من خلال مخطط شجرة الاحتمالات

باستخدام قاعدة الضرب

1. الحالة الاولي الصورة (head) والصورة (head) --> هي 1 * 1 ،فتكون النتيجة 1.
2. الصورة (head) و الكتابة (tail) --> هي 1 * 0 ،فتكون النتيجة 0 .
3. الكتابة (tail) والصورة (head) --> هي 0 * 1،فتكون النتيجة 0 .
4. الكتابة (tail) و الكتابة (tail) --> هي 0 * 0 ،فتكون النتيجة 0.

إذا جمعت ناتج عمليات الضرب أعلاه -لدينا (H ، H) هو 1 والباقي أصفار

تساعدنا شحرة الاحتمالات في إجابة الأسئلة المختلفة.

لنفترض أننا نرمي العملة مرتيين, احسب احتمال لو رمينا العملة مرتين ، فسنحصل على صورة (head) مرة واحدة فقط ؟

والإجابة هي 0.5.

فلنقم ببناء مخطط شجرة الاحتمالات لنفهم ذالك ،وبذالك يمكن حصر كل الاحتمالات في النتائج الاتية:

1. الاحتمال الأول الصورة (head) والصورة (head) --> هي 0.5 * 0.5 ،فتكون النتيجة 0.25.
2. الاحتمال الثاني الصورة (head) و الكتابة (tail) --> هي 0.5 * 0.5 ،فتكون النتيجة 0.25.
3. الاحتمال الثالث الكتابة (tail) والصورة (head) --> هي 0.5 * 0.5 ،فتكون النتيجة 0.25.
4. الاحتمال الرابع الكتابة (tail) و الكتابة (tail) --> هي 0.5 * 0.5 ،فتكون النتيجة 0.25.

أين يتم تمثيل الصورة (head) مرة واحدة فقط في الاحتمالات الاربعة ؟

فالنستبعد الاحتمال الاول والرابع فهمل لايفيان بالشرط , يتبقي لنا الاحتمالان الثاني والرابع وحدهما يفيان بالشرط فلنأخذ قيمة الاحتمالات 0.25 المرتبطة بهاتين الحالتين ونجمعها معًا ، مما يعطينا 0.25 +0.25= 0.5 هذا هو الرقم الصحيح لسؤالنا.

فلنجعل المثال أكثر تعقيداً ونرمي العملة (fair coin ) ثلاث مرات, ما هو أحتمالية أن نحصل علي صورة (head) مرة واحدة فقط خلال الثلاث رميات ؟

والأجابة ستكون شاقة قليلاً. وسنستخدام شجرة الاحتمالات لحل السؤال .

سنحصل من الرمية الأولى إما وجة الصورة (head) أو الكتابة (tail) ، وكذالكفي الرميات الثانية لكل احتمال من الرمية الاولي وكذالك في الثالثة لكل احتمال في الرامية الثانية، وإذا نظرت إلى هذا ، ستلاحظ أن كل المجموعات الممكنة ممثلة.

لدينا 8 حالات. إذن 8 × 1/8 لها مجموع 1.

كم عدد الحالات التي لديها وجه الصورة (head) مرة واحدة فقط ؟ تم التحقق من صحة ذلك في 3 حالات فقط.

يمكن أن تكون الصورة (head) في الموضع الأول ، أو في الموضع الثاني أو في الموضع الثالث فقط ، لذا فإن 3 من 8 حالات لها وجة الصورة (head) واحد فقط ، وبالتالي يكون الإجمالي من 3/8 وهو ما يساوي 0.375

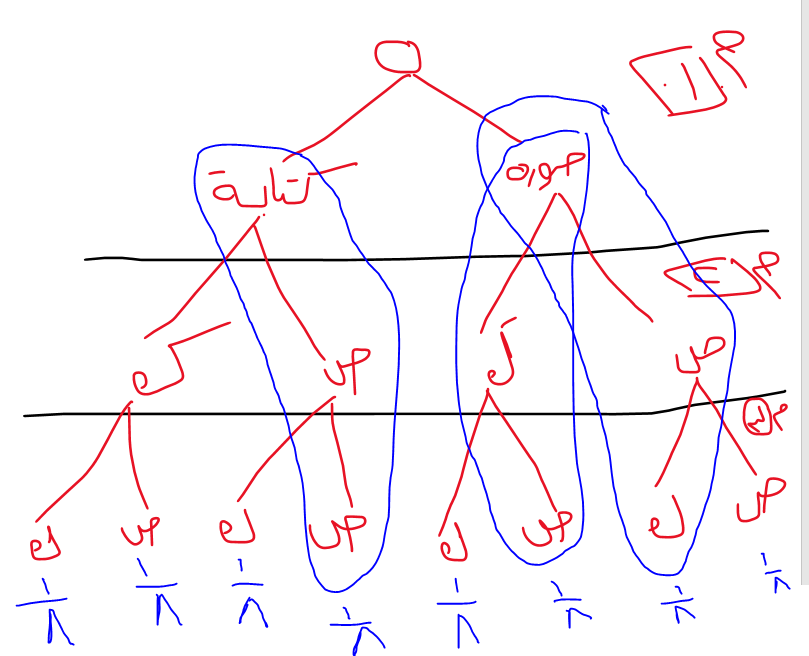
فلنجعل المثال أكثر صعوبة ،بإستخدام عملة متحيزة ( loaded coin) - احتمال H وجه الصورة (head) هو 0.6. قد تستغرق الإجابة بعض الوقت لحساب الاحتمال علي الورق . لكن كمل تعودنا بالضبط. نرسم شجرة الاحتمالات. ثم نقوم بتطبيق الضرب الذي أوضحناه سابقًا لحساب احتمال كل نتيجة ؛تذكر من الواضح أن H ، H ، H أكثر احتمالية من T ، T ، T و ، اجمع القيم المقابلة.

والإجابة هي 0.288. كيف حصلت عليه؟ دعونا نفحص هذه الحالات الثلاث الحرجة. HT T يساوي 0.6 لـ H مضروبًا في 0.4 لـ T و 0.4 أخرى لـ T الثاني وهذا يعطيني 0.096 الآن اتضح أن هذه الحالة هنا لها نفس الاحتمال لأن كل ما نفعله هو الترتيب 0 ، 4 × 0.6 × 0.4 ونحن اعلم أنه في عملية الضرب ، لا يهم الترتيب ، لذلك نحصل على نفس القيمة 0.096 ، واتباع نفس المنطق أيضًا ، يعطيني المنطق الثالث 0.096 ، لذا بجمع هذه 0.096 معًا ، أحصل على 0.288 ، فأنا لم أملأ جدول الحقيقة بأكمله ، كما فعلت في التطوير ، ملأت فقط الحالات التي تهمني ، ومع ذلك أحصل على النتيجة الصحيحة

لنقم بتمرين أخير بأستخدام حجر النرد (الزهر), ولاحظ الفرق بين النرد والعملة هو أن في النرد هناك6 نتائج محتملة بدلاً من إثنتين ،

ودعنا نفترض إنه نردًا متكافئ (fair die) مما يعني أن كل واجه للنرد يأتي باحتمال ثابت ، ما هو برأيك احتمال أن يعرض الرقم عددًا زوجيًا؟

يمكنك استخدام مخطط شجرة الاحتمالات لحساب هذه القيمة.

في مخطط شجرة الاحتمالات، نجد 6 نتائج، من 1 إلى 6. لكل منها احتمال متساوٍ من أصل ستة وهو السدس 1/6.

نصف هذه الأرقام زوجية 2 و 4 و 6، لذلك إذا جمعناها معًا، نحصل على

1/6+1/6+1/6=1/2.

كانت النتيجة 0.5, أي ما يعادل النصف.

الآن كاختبار أخير، سأسألك سؤال صعب حقًا. لنفترض أننا رمي هذا النرد مرتين. ماهو أحتمال التكرار (Double), يعني نحصل علي نفس الرقم في كلا الرميتين ؟.

ومرة أخرى يمكننا الإجابة باستخدام مخطط شجرة الاحتمالات الآن لدينا 36 احتمال مختلفًا ، 6 احتمالات للرمية ألأولي مضروبة في 6 احتمالات للرمية الثانية (يعني كل احتمال في الرمية الأولي سيكون مقرون بست احتمالات من الرمية الثانية )، وليس لدي مساحة كبيرة لرسم جميع الإدخالات الـ 36 ، لذا دعني أرسم فقط تلك التي ذات صلة ، واحد واحد ، اثنان اثنان ، وهكذا حتى ستة - ستة لكل منها احتمال 1/6 للنتيجة الأولى مضروبًا في 1/6 للنتيجة الثانية ، التي تعطيني 1/36 ، و نفس المنطق ينطبق على الآخرين بالنسبة لجميع الحالات الست لدينا احتمال 1/36 للحصول على النتيجة من خلال إضافتها أحصل على 1/6 ، لماذا؟ لماذا ، أحصل على 6 من 36 والتي يمكنني تبسيطها والحصول على 1/6 وهو ما يساوي 0.16667 لذا 1 من 6 مرات ستحصل على تكرار.

لقد تعلمت الكثير. تمكنت حقًا من اكتساب فهم أساسي للاحتمالات.

لقد تعلمت حساب احتمالات حدوث حدث (event)، مثل نتيجة رمي عملة معدنية.

تعلمت أن احتمال وقوع حدث معاكس هو 1 مطروحًا منه احتمال وقوع الحدث

وتعلمت ما هوالاحتمال المركب.

ما تعلمناه هنا يسمي الاحتمالات المستقلة مما يعني ببساطة أن نتيجة المحاولة الثانية للعملة لا تعتمد على نتيجة المحاولة الأولى.

في الدرس التالي ، سنتحدث عن الاحتمال الشرطي ، دعنا ننتقل ونغوص بشكل أعمق في حفرة الاحتمالات.

مصادر إضافية:

https://arabiska.matteboken.se/lektioner/skolar-9/sannolikhet-och-statistik/sannolikhet